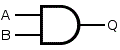コンピュータ技術者のための無料情報倉庫です

ソフトウェア技術者向け情報

4. コンピュータの計算方法
・・・コンピュータが実行する計算方法・・・

　本稿は、コンピュータが計算する仕組みについて概説します。 近年では、コンピュータ言語と機器性能の進歩で、ほとんどの場合、ユーザは意識する必要がなくなってきました。 （解析・評価・設計などの特殊な場合に、今日でも仕組みの知識が必要になります。）
　シャノンの論文とノイマンのグループの成果により二つの事柄があきらかです。 一つは、すべての情報（データやプログラム）は2進数としてコンピュータに保存されています。 特に、マイナスの数値は「補数」の形で保存されており、桁あふれを利用することで、引き算を足し算として計算しています。 二つは、集合の演算原理であるブール代数の法則で計算回路を構成しています。 特に、基本の回路は三つのみで、すべての計算は組み合わせによって実施しています。

4-1.ブール代数

　計算を実行するためには、最低2つの集合が必要です。 2つ以上の集合を使用して集合の計算法則が成立します。（注1）

注1：
イギリスの数学者 ブール(George Boole) が1854年の著書「思考の法則に関する研究」で 提唱した記号論理学を ブール代数(Boolean algebra) と呼びます。

(1) 文章を構成するための情報
　文章を構成する要素（言葉）は、その文章を使用するための「目的」が明確である必要があります。多くの設計書書式では、冒頭に「目的記述」を定義することを要求しています。（特に、オブジェクト指向設計書では、内容を把握するための重要事項として、必須要件と定義しています。） 目的の明確でない文章は、読み手ごとに異なる内容を示唆してしまう可能性を排除できないことに問題があるのです。
また、記述する内容は、「過不足なく」を玉条とします。不必要な記述は、無駄であるばかりでなく、読み手に混乱や誤解を招く恐れがあります。不十分な記述（当たり前だから記述しない）は、漏れや過誤などの不正確さの原因となります。
ゆえに、正しい文章は、目的に向けて過不足のない記述と定義することができます。
(2) 文章の形式
コンピュータ関連業務用文章（以下、単に「文章」と表現します。）には、コンピュータもしくはその利用者に性格な情報を伝達することを目的として、3つの基本ルールが存在します。
（著者の独善で3つにさせていただきました。本稿のみの話です、あしからず。）
「3つの基本ルール」
・文章は、平叙文の形式（主語+述語）で記述してあり、主語と述語は集合で表現可能である。
・文章は、命題の形式で記述でき、したがって、対偶が成立する。
・文章は、1H5Wの要素（注1）を、過不足なく含んでいる。
これらで構成された文章は、コンピュータおよび利用者、開発者に、命令（プログラム：処理をする手順）と情報（データ：処理をする対象）を正確に処理する方法を示唆します。

注1：
how、who、when、where、what、whyのことです。（念のため）

(2) 基本の集合演算
　ブール代数の基本演算は、次の3通り（and、or、not）だけです。 シャノンの論文の骨子は、ブール代数と2進数で、すべての演算は3つの基本演算の組み合わせであることです。
集合A、Bの二つを使用して解説します。

「and演算」

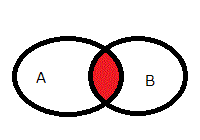
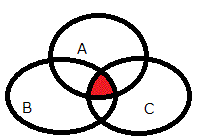
・and演算
アンド演算と読みます。
集合（数学）では「論理積（ろんりせき）」と呼び、
A∧B、または、A and B
などと記述します。
右図で、色付きの部分（集合AとBの共通部分）を示します。
論理演算（注2）では、AとBが等しく「真：1であらわす」であるとき結果は「真」、 その他の場合（3通り）は、「偽：0であらわす」となります。

「or演算」

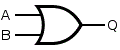
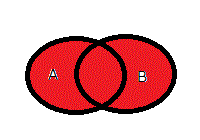
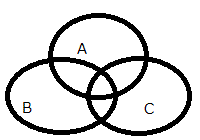
・or演算
オア演算と読みます。
集合（数学）では「論理和（ろんりわ）」と呼び、
A∨B、または、A or B
などどと記述します。
右図で、色付きの部分（集合AとBの全て）を示します。
論理演算では、AとBのいずれか「真：1であらわす」であるとき（3通り）結果は「真」、 その他の場合（1通り）は、「偽：0であらわす」となります。

「not演算」

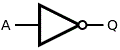
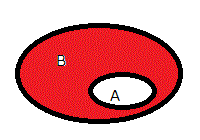
・not演算
ノット演算と読みます。
集合（数学）では「論理否定（ろんりひてい）」と呼び、〜A、notA、または、Aの上に横線をひいて記述します。
右図で、色付きの部分（集合A以外の全て）を示します。
ここで集合Bは、全体を表します。（全体集合と呼ぶ） 論理演算（注11）では、A「真：1であらわす」であるとき結果は「偽：0であらわす」、A「偽」のとき結果は「真」となります。

注2：
論理演算は、「1」と「0」を用いる論理で、2値代数、2値論理数学、ディジタル代数、スイッチング代数などとも呼ばれます。
便宜的に、「1」を真、「0」を偽と呼ぶ場合もあります。

(2) ブール代数の演算規則：参考
コンピュータの計算ルールはブール代数と呼ばれる、集合の四則演算で定義しています。 通常の数値計算とすこし異なる部分もありますのでご注意ください。
論理和：足し算（2項演算子とよびます）は「+」（または、「∨」:or）、
論理積：掛け算（2項演算子とよびます）は「・」（または、「∧」:and）、
論理否定：補（単項演算子とよびます）は「not」で表します。
集合A、B、C、0（空集合：要素なし）、1（普遍集合：全体を表す）の五つを使用して示します。
「4つの基本ルール（公理から抜粋）」
・　交換法則
　　A + B = B + A　、および、A・B = B・A
・　分配法則
　　A・( B + C ) = ( A・B ) + ( A・C )　、
　　および：次は要注意（数値演算とは異なります）、
　　A + ( B・C ) = ( A + B )・( A + C )
・　単位元
　　A + 0 = A　、および、A・1 = A
・　補元
　　A + notA = 1　、および、A・notA = 0
分配法則は、数値演算と異なる公式が含まれています。
ベン図にて確認可能です。

(3)　設計書等の記述上の注意点
ブール代数（集合）を表現する「論理式」は、日常使用する「用語」では、曖昧さを残してしまう場合があるので、注意が必要です。
曖昧な例：
「オブジェクト指向設計では、不要なものは作成しない。」
解釈1：作成したものは必要であるが、必要なものをすべて作成するか否かは問わない。
解釈2：作成したものは必要であり、かつ、必要なものをすべて作成する。
このように、二通り以上の解釈が可能な文章は「好ましくない」ことに留意していただきたい。 著者の経験では、少なくとも書きなれるまでは、文章と対偶のベン図を描いて確認することが有効です。 設計途上では解釈1をとり、設計終了時点で解釈2をとるのであれば、コンピュータにも理解できるように、2文に分けて記述するべきです。

4-2.計算回路

・・・コンピュータの仕組みの基本となる計算回路・・・

実際のコンピュータの回路では、多くの回路を使用しています。 例として、最も単純な一桁の2進数の足し算の回路（半加算器と呼びます）のうち、最も単純なものを紹介します。 使用する回路は、論理積(and)、論理和(or)、論理否定(not)の三種類です。
この3回路を組み合わせて、もっとも単純な2進数の足し算が可能です。
0+0=0、0+1=1、1+0=1、1+1=10 が実行可能であればよいですね。
答えは、2桁になる場合があるので、桁ごとに分解します。 足し算の左辺を集合A、足し算の右辺を集合Bとします。 答ののほうは、一桁目（2⁰）を集合S、二桁目（2¹）を集合Cとします。

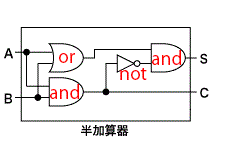
0+0のとき、C=0、S=0
0+1のとき、C=0、S=1
1+0のとき、C=0、S=1
1+1のとき、C=1、S=0
となります。
AとBに「0」か「1」をあてはめて、確認してください。

【あとがき】
コンピュータに言葉を理解させるのは、慣れてしまうまでは、面倒なものです。
しかしながら、技術者諸氏にもっとも注意を払っていただきたいのは、人と人のコミュニケーションなのです。 年代や勤務場所によって、異なる文化を「あたりまえ」の日常としています。
人とコンピュータとの共通の「言語」として、2進数、集合とブール代数をご紹介しました。 これを、人と人とのコミュニケーションにもご活用いただきたいのです。
記号や語句の細かい意味が、現場によって異なることを、ベテランの技術者ならばご経験あることと存じます。 そんなおりは、是非、命題とベン図でも書いて、内容の確認を実施てくだされば、欣快に存じます。

コンピュータの計算方法-以上

お問い合わせについて

▲ページトップに戻る

ホーム　|　提供情報　|　著者情報　|　お問い合わせ

Copyright (C) 2015 SEの独り言 All Rights Reserved.　design by tempnate